Intrinsic Dimension of Data Representations in Deep Neural Networks

This paper studies the geometrical properties of the representations learned by neural networks. Published at NeurIPS 2019.

Intrinsic dimension (ID) is viewed as a fundamental geometric property of a data representation in a neural network. Informally, it is the minimal number of coordinates which are necessary to describe its points without significant information loss. This paper introduces some existing observations on the ID of some neural networks:

• Linear estimates of ID on simplified models and local estimates of ID have been developed.
• Local ID has been shown correlates with the adversarial robustness. Lower local ID -> higher robustness.
• Local ID at several locations on the tangent space of object manifolds are estimated, and found decrease along the last hidden layers of AlexNet.
• Local ID in the last layer of DNNs has been found to be much lower than the dimension of the embedding space.
• Some linear and nonlinear dimensionality reduction techniques have been developed.

This paper aims to answer:

• How the ID changes alongs the layer of CNNs?
• How different is the actual ID from the ‘linear’ dimensionality of a network?
• How is the ID relates to the generalization performance?

They uses an existing method, TwoNN, to estimate global ID. It exploits the fact that nearest-neighbour statistics depend on the ID. Based on TwoNN, The answers are shown to be:

• The variation of the ID along the hidden layers of CNNs follows a similar trend across different architectures: increase in early layers, then monotonically decrease.
• ID of CNNs are typically several orders of magnitude lower than the dimensionality of the embedding space (the number of units in a layer).
• In networks trained to classify images, the ID of the training set in the last hidden layer can accurately predicts the network’s classification accuracy on the test set: the lower the better. ID remains high for a network trained on non predictable data (i.e., with permuted labels).

These observations seem to be consistent with our intuition of ID. Now we study how the ID is calculated in this paper.

Estimating the ID by TwoNN

TwoNN ¹ is based on computing the ratio between the distances to the second and first nearest neighbors (NN) of each data point. It can be applied even if the manifold containing the data is curved, topologically complex, and sampled non-uniformly.

The assumption of TwoNN: the density is constant on the scale of the distance between each point and its second nearest neighbor.

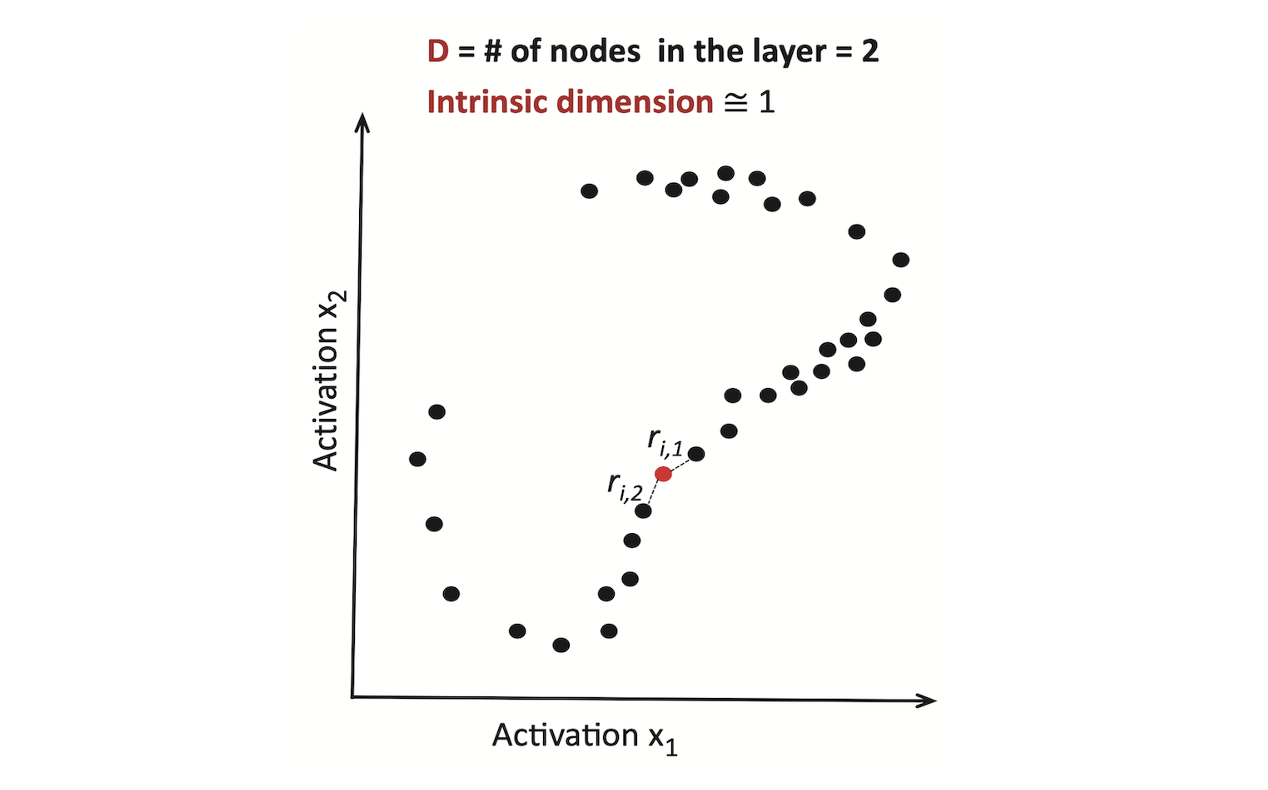
Let points $x_i$ be uniformly sampled on a manifold with intrinsic dimension $d$ and let $N$ be the total number of points. The algorithm of TwoNN consists of the following steps:

• For each data point $i$ compute the distance to its first and second neighbour $r_i^{(1)}$and $r_i^{(2)}$, as shown in the figure above.

• Compute the ratio $\mu_i = r_i^{(2)} / r_i^{(1)}$. It follows a Pareto distribution with parameter $d+1$ on $[1, +\infty]$. $P(\mu) = \frac{d}{\mu^{1+d}}$. ${\mu_i}$ are assumed $i.i.d.$.

• Infer $d$ by maximizing the empirical likelihood: $$ P(\boldsymbol{\mu} \mid d)=d^{N} \prod_{i=1}^{N} \mu_{i}^{-(d+1)} $$

• Repeat the calculation selecting a fraction of points at random. This gives the ID as a function of the scale of the distances.

It is introduced in this paper that:

1. The ID can also be estimated by restricting the product in the above equation to non-intersecting triplets of points, for which independence is strictly satisfied, but, as shown in the paper ¹, in practice this does not significantly affect the estimate.
2. The ID estimated by this approach is asymptotically correct even for samples harvested from highly non-uniform probability distributions.
3. When ID is smaller than 20, the estimated values remain very close with finite samples; when larger ∼ 20, the estimated values should be considered as lower bounds.
4. ID should be at least approximately scale invariant. To test that, they systematically decimating the dataset, thus gradually reducing its size and the average distance between data points had become progressively larger.